Fayl:Pm1234 Euler.svg
Faylın orijinalı (SVG faylı, nominal olaraq 240 × 390 piksel, faylın ölçüsü: 26 KB)
Bu fayl Wikimedia Commonsdandır və başqa layihələrdə də istifadə edilə bilər. Faylın təsvir səhifəsindəki məlumat aşağıda göstərilib.
Xülasə
| İzahPm1234 Euler.svg |
English: Euler summation of 1 − 2 + 3 − 4 + · · · to 1/2-1/4.
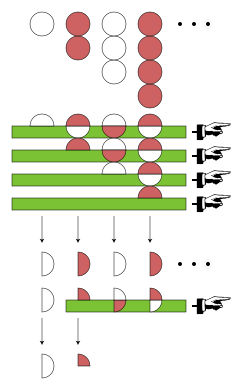
The original series 1 − 2 + 3 − 4 + · · · is depicted at the top of the diagram; the Euler transformed series 1/2 − 1/4 + 0 + 0 + · · · is depicted at the bottom of the diagram. The conclusion is that the Euler sum of 1 − 2 + 3 − 4 + · · · is 1/2-1/4 = 1/4. Only the first four terms of the series are shown. A white disk represents +1; a reddish disk represents −1. The units are grouped on top of each other as they occur within the terms of the series. Let a = 1 − 2 + 3 − 4 + · · · be the original formal series. Let S be the shift operator on formal series, Let T be the average between S and the identity operator: Then given a series a, if it converges, then its sum is the same as the sum of the series The Euler summation procedure has many descriptions, but for the present purposes it can be described as a repetition of the above "process". To be precise, the nth term of the Euler transformed series is See eq. (20.3) of Korevaar, Jacob (2004) Tauberian Theory: A Century of Developments, Springer, pp. 326 ISBN 3-540-21058-X To compute this transform in place, one pulls half of each term into the next term, then fixes the first term, then repeats. The part of the diagram with the four green stripes indicates taking half of every term in the original series a and pulling it into the next term. Most of the units cancel, leaving the series The first term of this series is fixed, leaving The process repeated upon the remaining terms, leaving 1/2 − 1/4 + 0 + 0 + · · ·. Now two terms are fixed, and the remaining terms are all zero, so all further applications of T do not change the series, and they are not depicted. In the visual language, subsequent green stripes pull on nothingness. The result is the Euler transformed series, 1/2 − 1/4 + 0 + 0 + · · ·. It is convergent, having only two nonzero terms, and its sum is 1/2 − 1/4. The diagram does not distinguish between the finite series and its sum. As a number, 1/2 − 1/4 = 1/4. The above is done to illustrate how Euler summation works on the series. In practice, one exploits auxiliary quantities, and the computation is much easier; see for example Image:Pm1234-Euler1755.png. An extended description of Euler's procedure on 1 − 2 + 3 − 4 + · · ·, including reversing its alternation and taking iterated forward differences, is at w:1 − 2 + 3 − 4 + · · ·#Euler and Borel. |
| Tarix | |
| Mənbə | User created |
| Müəllif | User:Melchoir |
| Digər versiyalar | PNG version |
Lisenziya

|
Bu sənədi GNU Azad Sənədləşdirmə Lisenziyası, Versiya 1.2 və ya Azad Proqram Fondu tərəfindən nəşr olunan hər hansı sonrakı versiya şərtlərinə əsasən dəyişməz bölmələr, ön qapaq mətnləri və arxa qapaq mətnləri olmadan köçürmək, yayımlamaq və / və ya dəyişdirmək üçün icazə verilir; Lisenziyanın bir nüsxəsi GNU Azad Sənədləşdirmə Lisenziyası adlı hissəyə daxil edilmişdir.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
| Bu fayl Creative Commons Attribution-Share Alike 3.0 Unported lisenziyası altında yayımlanır. | ||
| ||
| This licensing tag was added to this file as part of the GFDL licensing update.http://creativecommons.org/licenses/by-sa/3.0/CC BY-SA 3.0Creative Commons Attribution-Share Alike 3.0truetrue |
- Siz heç bir məhdudiyyət olmadan:
- paylaşa bilərsiniz – əsəri köçürə, paylaya və ötürə bilərsiniz
- remiks edə bilərsiniz – əsəri adaptasiya edə bilərsiniz
- Aşağıdakı şərtlərə əməl etməklə:
- istinad vermək – Müvafiq istinad verməli, lisenziyaya keçid əlavə etməli və dəyişikliklər edilib-edilmədiyini bildirməlisiniz . Siz bunu istənilən şəkildə edə bilərsiniz, lakin lisenziya verənin sizə şəxsən icazə verdiyini göstərən formada yox.
- bənzər paylaşma – Əsəri remix edirsinizsə, dəyişdirirsinizsə və ya üzərində iş aparırsınızsa, öz töhfələrinizi orijinalda olduğu kimi eyni və ya uyğun lisenziya altında yayımlamalısınız.
Captions
Items portrayed in this file
təsvir edir
copyright status ingilis
copyrighted ingilis
4 mart 2007
Faylın tarixçəsi
Faylın əvvəlki versiyasını görmək üçün gün/tarix bölməsindəki tarixlərə klikləyin.
| Tarix/Vaxt | Kiçik şəkil | Ölçülər | İstifadəçi | Şərh | |
|---|---|---|---|---|---|
| indiki | 13:43, 1 yanvar 2008 |  | 240 × 390 (26 KB) | wikimediacommons>Papa November | Removed unnecessary Adobe Illustrator metadata. May fix rendering problems. No copyright claimed for non-creative derivative work. |
Fayl keçidləri
Aşağıdakı səhifə bu faylı istifadə edir:




